经典滑模控制趋近律收敛性的理解
本文部分参考AI内容,仅作为个人理解使用,严谨分析请查阅相关文献
在经典的滑模控制中,考虑问题
$$ \ddot{e}(t)=u(t)+\delta(t) $$其中,$e(t)$为系统的误差, $u(t)$为控制输入, $\delta(t)$为系统的有界扰动,定义$\bar{\delta}=\sup_t\|\delta(t)\|$,这里$\sup$表示上确界,即扰动的范数(此处为标量系统即为绝对值)的最大值。 滑模控制的核心思想之一是降阶,将原来的一个二阶系统转换为两个一阶子系统(分别对应两个阶段)。 经典的滑模控制中,首先设计一个滑模面$s(t)=\dot{e}(t)+a e(t)$, 其中$a>0$。 所设计的控制律为:
$$ u(t)-k\operatorname{sgn}(s)-a \dot{e}(t) $$从系统的轨线的角度,如下图,整个闭环系统的过程可以分为两个阶段:
- 趋近阶段:首先在有限时间上收敛到所设计的滑模上,其动态为公式(eq 1),包含扰动
- 滑动阶段:再在滑模面上收敛到期望的平衡点,其动态为$\dot{e}=-a e(t)$,不含扰动。
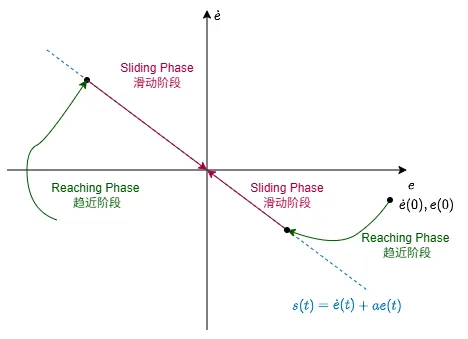
针对这两个阶段有这些值得关注的:
- 趋近律中的$\operatorname{sgn}(e)$函数,在标量的情况(本文)通常选取符号函数,在多维向量的情况有两种表达,一种是逐元素的定义,一种为基于范数的定义,如果使用的是二范数,那么表示向量的单位向量。由于符号函数是非连续函数,系统会有震颤chattering的问题,于是有了减少和抑制震颤的一些方案:
- 减少震颤:通常为用连续的函数替代sign,这样会牺牲收敛精度,一般称作边界层法(boundary layer),即不再收敛到滑模面$s=0$而是收敛到这个滑模面的一定距离的边界内;
- 抑制震颤:主流为使用高阶滑模,这样会牺牲部分抗扰的能力。如使用二阶滑模算法,通常只能抵抗导数有界的扰动。
- 这里的滑动阶段使用的是线性滑模,所以系统状态渐进收敛,如果需要有限时间收敛,可以使用终端滑模$s=\dot{e}+|e|^{\alpha}\operatorname{sgn}(e)$, $0<\alpha<1$。但是终端滑模会有歧义的问题,改进方案有非奇异终端滑模。
- 图片中这是经典的相轨迹图,在横轴上方$\dot{e}(t)>0$,$e(t)$增加,系统状态向右变化,反之,在横轴下方$\dot{e}(t)<0$,$e(t)$减少,系统状态向左变化,系统总体有一个顺时针变化的趋势。线性滑模的线性在图中体现为$s=\dot{e}(t)+a e(t)$为一条直线,斜率$-a$为负,保证系统稳定。在直线上方满足$s>0$在直线下方满足$s<0$.
到达阶段的系统其实就是一个线性系统,不存在扰动了,现代控制理论或者经典控制理论都可以很容易地分析。
但是趋近阶段有sign函数和扰动函数,这是一个时变非连续系统,系统不能再经典意义下理解。
常见的趋近阶段分析方法
一般网上的教程分析趋近阶段都是采用这样一个Lyapunov函数:
$$ V=\frac12 \|s\|^2 $$对这样的函数求导可得:
$$ \begin{aligned} \dot{V} &=s\dot{s}=s\left(-k\operatorname{sgn}(s)+\delta(t)\right)\\ &=-k\|s\|+s\delta \leq -k\|s\|+\|s\| \|\delta\|\\ &\leq -(k-\bar{\delta})\|s\| \end{aligned} $$这里使用了条件$\sup_t\|\delta(t)\|< \bar{\delta}$. 于是我们应用Lyapunov 定理得到$s\to 0$.
实际滑模控制中,滑动阶段是有限时间内的,所以还需要证明$s$在有限时间内收敛到零。 刚刚的分析,我们可以得到:
$$ \dot{V}=\frac{dV}{dt}\leq-(k-\bar{\delta})\sqrt{2V} $$为了求解该标量微分方程的解,我们需要对$V$分情况讨论。
情况一:当$V\neq 0$时,可以通过分离变量可得:
$$ V^{-1/2}dV\leq-(k-\bar{\delta})\sqrt{2}dt $$同时积分得:
$$ 2V^{1/2}(t)-2V^{1/2}(0)\leq-(k-\bar{\delta})\sqrt{2}t $$从这个式子可以看出,最晚在$t=\frac{2V^{1/2}(0)}{(k-\bar{\delta})\sqrt{2}}$的时候,系统的$V(t)$收敛到零。
情况二:当$V=0$时,显然$\dot{V}=0$,此后$V$恒等于零。
综上所述,$V=\frac12 \Vert s \Vert^2$在有限时间收敛到零,在此时间后$V$保持为零。 Barbalat’s Lemma 告诉我们当$s\to 0$ 的时候,如果$\dot{s}$是一致连续的,那么有$\dot{s}\to 0$。 这里显然不满足该一致连续的条件。
那么,在有限时间$s$ 收敛到$0$后,是否有$\dot{s}$也收敛到零呢? 如果$\dot{s}$也收敛到零,是否意味着$k\operatorname{sgn}(x)$收敛到扰动$\delta(t)$呢?
扰动是被sign函数抵消了吗?
在滑模控制的书籍中,通常会提到一个概念等效控制,会提到$\dot{s}$有限时间在平均意义下收敛到零。 一直以来,我不理解这句话的具体含义,结合chatgpt等的分析,这里试图解释以下: 对于上午提及的滑动阶段的系统方程:
$$ \dot s = -k \operatorname{sgn}(s) + \delta(t) $$在经典解的理解下,从逐点角度(pointwise)分析:
- $\operatorname{sgn}(s) \in \{-1,+1\}$
- $\delta(t) \in [-\bar{\delta},\bar{\delta}]$ 因此显然有: $ \operatorname{sgn}(s) \neq \delta(t) \quad \text{for almost all } t $ 确实,两者不相等。 但这并非滑模控制理论所主张的结论。
在系统的Filippov解意义下,系统的解应该满足微分包含方程
$$ \dot s = \begin{cases} -k + \delta(t), & s>0 \\ +k + \delta(t), & s<0 \end{cases} $$在 $s=0$ 处,Filippov定义:
$$ \dot s \in \operatorname{co}\{-k+\delta(t), k+\delta(t)\} $$这里的$ \operatorname{co}$表示集合内部元素组成的凸包,对于本文的场景可以理解为这两个点练成的线段上的所有点的集合,也就是: 当$s=0$时, $\dot s \in [-k+\delta(t), k+\delta(t)]$. 显然,$\dot s = 0$满足这个区间,也就是说$\dot s = 0$是微分包含系统在 $s=0$ 处的一个可接受Filippov速度。 这保证了滑模运动的存在性。
实际的控制信号仍然是:
$$ -k\operatorname{sgn}(s(t)) \in \{-k,+k\} $$但在滑模阶段:$s(t)$ 围绕0做无穷快振荡;$\operatorname{sgn}(s(t))$ 做无穷快切换。 时间平均满足:
$$ \langle k\operatorname{sgn}(s) \rangle = \delta(t) $$- 📌 这不是逐点收敛,而是弱(平均)收敛。
- 📌 This is not pointwise convergence, but weak (averaged) convergence.
从物理直觉上理解,可以理解为占空比调制(duty cycle modulation):
- 当 $\delta (t) > 0$ 时:$s>0$ 的持续时间更长
- 当 $\delta (t) < 0$ 时:$s<0$ 的持续时间更长
两侧的时间占比会自动调整,使得:
$$ k\operatorname{Sgn}\text{的平均切换效应} = \delta(t) $$通常,理解为可以使用一个低通滤波器将信号$k\operatorname{sgn}(s)$滤波后近似等于$ \delta(t)$.
小节:在滑模中,不连续项并非逐点收敛到扰动;其平均效应抵消了扰动,这一过程由Filippov凸化方法描述。
Fillipov意义下的趋近阶段分析方法
基于上面的分析,在学术论文中通常会说系统需要在 Filippov 意义下理解。 直观来说,原来的经典解是需要找满足(eq 1)这个微分方程的$s(t)$。 而Filippov 意义下的解则为需要满足(eq 1)对应的Filippov微分包含的$s(t)$。 该微分包含定义为(eq 2)
$$ \dot{s}\in -k \operatorname{Sgn}(s)+\delta(t) $$其中
$$\operatorname{Sgn}(s)=\begin{cases} \{-k\} & s>0\\ [-k,k] & s=0\\ \{k\} & s<0 \end{cases} \tag{eq 2} $$对于系统$\dot{x}=X(x)$,其经典解和Filippov解的对比如下表所示, 对于函数$\operatorname{sgn}(x)$其显然不是一个关于$x$连续的函数,因此其不存在连续可微的经典解。
| 类型 | 解的性质 | 存在性条件 | 唯一性条件 |
|---|---|---|---|
| 经典解 | 连续可微 | \( X: \mathbb{R}^d \to \mathbb{R}^d \) 连续 | 在 \( B(x,\varepsilon) \) 上本质单边Lipschitz¹ |
| Filippov解 | 绝对连续 | \( X: \mathbb{R}^d \to \mathbb{R}^d \) 可测且局部本质有界 | 命题4&5 |
对于这样的微分包含系统(eq 2)使用Lyapunov 方法分析,需要使用广义导数,记为$\dot{\tilde{V}}$。 其与原始微分方程系统(eq 1)的关系为:$\dot{V}\in\dot{\tilde{V}}$。 所选取的Lyapunov 函数仍然是上面的$V$,其广义导数为:
$$ \begin{aligned} \dot{V}=s\dot{s}\in\dot{\tilde{V}} &=s\left(-k\operatorname{Sgn}(s)+\delta(t)\right)\\ &=-k\|s\|+s\delta \leq -k\|s\|+\|s\| \|\delta\|\\ &\leq -(k-\bar{\delta})\|s\| \end{aligned} $$此后$s$有限时间收敛的分析方法与常见的分析方法一样,Filippov 的方法主要是解释了$\dot{s}$的收敛性问题。
齐次度系统的讨论
上面通过Lyapunov 的方法讨论了趋近阶段有限时间收敛的问题,在文献通常还会利用齐次系统的理论来分析趋近过程,证明有限时间收敛的问题。
对于系统$\frac{\partial s}{\partial t}\in -k\operatorname{Sgn}(x)$, 使用一组变量$(\kappa^m x, \kappa^n t)$替换掉$(x,t)$,可以知道当$m=1$,$n=1$的时候,这个微分包含表达式仍然成立。 通常这里记$x$的齐次度为$\operatorname{deg}(x)=1$,系统的齐次度为$-\operatorname{deg}(t)=-1$. (这里$x$的齐次度可以任意取整数值,对应系统的齐次度即时间$t$的齐次度的相反数,具体定义可参考wikipedia)。
在齐次系统中有负齐次度的系统的如果渐近稳定,那么其也有限时间稳定。 上面使用Lyapunov 方法已经分析了系统渐近稳定,那么即可找到集合$D_1$,$D_2$和时间$T$,使得对于所有从$D_1$开始的系统状态最终都会收敛到$D_2$,并且$t>T$后系统始终在$D_2$内部。 此处考虑一维标量情况,记$D_1=[-d_1,d_1]$ 和$D_2=[-d_2,d_2]$。 任意的状态$x\in D_1$,将在时间$T$内收敛到$D_2$内。 令$x=\kappa \chi$,也就有任意的状态$\kappa \chi\in D_1$,将在时间$T$内收敛到$D_2$内。 也就是说:任意的状态$\chi \in [-d_1/\kappa,d_1/\kappa]$,将在时间$T/\kappa $内收敛到$D'=[-d_2/\kappa,d_2/\kappa]$内。 令$\kappa=d_1/d_2$,可知任意的状态$\chi \in [-d_2,d_2]$,将在时间$ d_2/d_1 T$内收敛到$D_3=[-d_2^2/d_1,d_2^2/d_1]$内。 于是,我们知道最终的收敛时间为$T_{1}=T+Tq+Tq^2+\dots=T/(1-q)$, 其中$q=d_2/d_1$.
小结
本文通过经典二阶双积分模型的滑模控制案例,讨论滑模的趋近阶段的有限时间收敛性质, 阐述非光滑控制中常见的Filippov解,等效控制,齐次度系统等理论。