非线性动态系统理论是滑模控制的重要理论基础,也是我学习滑模的最大障碍。 我决定花一些时间从工科本科数学知识出发整理非线性动态系统中的一些概念。 这篇笔记主要回顾连续性的定义,同时介绍传统的连续可微的classical解在应对非连续系统时存在性与唯一性的缺陷。
前言
最近在看滑模控制的文章,其中对于非连续系统的论述多有不解,比如如下Filippov微分包含到底是什么意思,
定义 2.2 A $\dot{x}\in F(x), x\in R^n$, is called a Filippov differential inclusion
- noempty 非空,
- closed+locally bounded=compact 紧集(有界闭集),
- convex 凸集,
and the set-value map $F$ is upper-semi-continuous(the maximal distance of the point of $F(x)$ and $F(y)$vanishes when $x\to y$).Solutions are defined as absolutely continuous functions of time satisfying the inclusion almost everywhere.
我也经常听到“Filippov 微分包含的解的所有广为人知的性质(existence,extendability etc)但是不包含唯一性(uniqueness)”,结合以下材料,打算整理一下所学内容:
- 知乎讨论:请问filippov解大概是什么意思?是怎么定义的?有什么作用? https://www.zhihu.com/question/55951952
- 主要是翻译的这个文献:CORTES J. Discontinuous dynamical systems[J/OL]. IEEE Control Systems Magazine, 2008, 28(3): 36-73. DOI:10.1109/MCS.2008.919306.
- HAN Z, CAI X, HUANG J. Theory of control systems described by differential inclusions[M/OL]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2016[2023-12-17]. http://link.springer.com/10.1007/978-3-662-49245-1.
回顾1:经典非线性系统解的条件
经典非线性系统的解存在性和唯一性需要微分方程右端Lipschitz连续, 一个使用较多的数学表述是khalil的非线性控制的引理1.3:
设$f(t,x)$关于$t$是分段连续的, 并且对所有$t\ge t_0$,在关于$x$的区域$D\subset \mathbb{R}^n$上$f(t,x)$是局部Lipschitz连续的。 设$W$是$D$中的一个紧子集,$x_0\in W$,并进一步设
$$ \dot{x}=f(t,x),x(t_0)=x_0 $$的解$t\ge t_0$时都在$W$内,那么这个解是$t\ge t_0$的唯一解。
回顾2:连续性
那么什么是Lipschitz连续呢,各种连续的关系又是什么呢,我们讨论的非连续动态微分方程又如何定义呢? 为了简便,这里用的是函数来叙述,如果是多变量函数或者泛函需要使用范数替代绝对值。
点连续与间断点
设函数$y=f(x)$在点$x_0$的某一邻域内有定义, 并且$\lim_{x\to x_0}f(x)=f(x_0)$, 那么就称函数$f(x)$在点$x_0$处连续。
借此可以定义函数不连续和间断点的概念:
设函数$f(x)$在点$x_0$的某去心领域内有定义, 在此前提下,如果函数$f(x)$有一下三种情形之一
- 在$x=x_0$处没有定义
- 在$x=x_0$处有定义,但$\lim_{x\to x_0} f(x)$不存在
- 在$x=x_0$处有定义,$\lim_{x\to x_0} f(x)$存在,但$\lim_{x\to x_0}\neq f(x_0)$ 那么函数$f(x)$在点$x_0$为不连续,$x_0$是函数$f(x)$的间断点。
函数的间断点可以分为
- 第一类间断点:左右极限都存在
- 可去间断点:左右极限都存在且相等
- 跳跃间断点:左右极限都存在但不等
- 第二类间断点:左右极限至少有一个不存在
- 震荡间断点:$\lim_{x\to\ x_0} f(x)$振荡不存在
- 无穷间断点:$\lim_{x\to\ x_0^+} f(x)=\infty$或$\lim_{x\to\ x_0^-} f(x)=\infty$
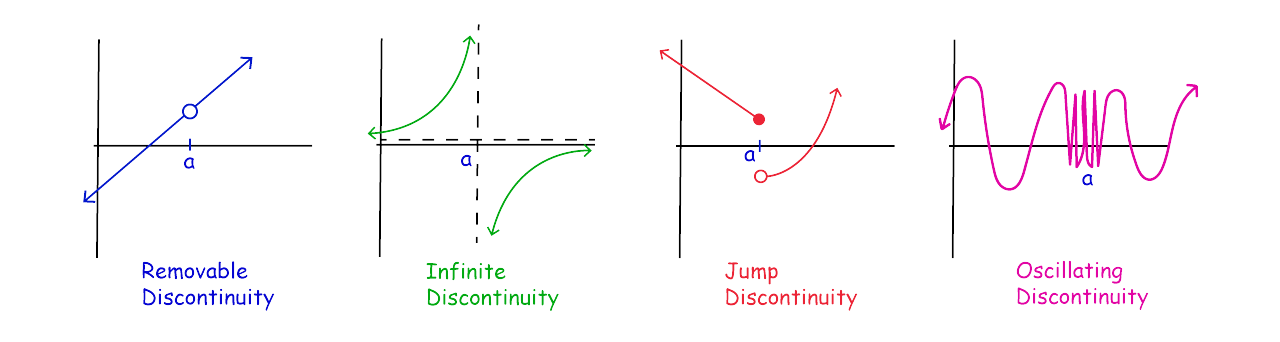
区间上连续相关的概念
以下借助豆包回顾一下区间上连续相关的概念
1. 连续(Continuous)
设\(f: [a,b] \to \mathbb{R}\),对任意\(x_0 \in [a,b]\),\(\forall \epsilon > 0\),\(\exists \delta > 0\)(依赖于\(x_0\)和\(\epsilon\)),当\(|x - x_0| < \delta\)时,有\(|f(x) - f(x_0)| < \epsilon\)。
2. 一致连续(Uniformly Continuous)
设\(f: [a,b] \to \mathbb{R}\),\(\forall \epsilon > 0\),\(\exists \delta > 0\)(仅依赖于\(\epsilon\),不依赖于\(x_0\)),对任意\(x_1, x_2 \in [a,b]\),当\(|x_1 - x_2| < \delta\)时,有\(|f(x_1) - f(x_2)| < \epsilon\)。
3. 绝对连续(Absolutely Continuous)
设\(f: [a,b] \to \mathbb{R}\),\(\forall \epsilon > 0\),\(\exists \delta > 0\),对任意有限个互不重叠的开区间\(\{(x_i, y_i)\}_{i=1}^n\),当\(\sum_{i=1}^n (y_i - x_i) < \delta\)时,有\(\sum_{i=1}^n |f(y_i) - f(x_i)| < \epsilon\)。
4. Lipschitz连续(Lipschitz Continuous)
设\(f: [a,b] \to \mathbb{R}\),存在常数\(L > 0\)(Lipschitz常数),对任意\(x_1, x_2 \in [a,b]\),有\(|f(x_1) - f(x_2)| \leq L |x_1 - x_2|\)。
5. 可导(Differentiable)
设\(f: [a,b] \to \mathbb{R}\),对任意\(x_0 \in (a,b)\),极限\(f'(x_0) = \lim_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}\)存在;闭区间端点处指单侧导数存在。
6. 连续可导(Continuously Differentiable,\(C^1\))
\(f\)在\([a,b]\)上可导,且导数\(f': [a,b] \to \mathbb{R}\)是连续函数。
7. 光滑(Smooth,\(C^\infty\))
\(f\)在\([a,b]\)上任意阶导数都存在且连续。
区间上连续相关的概念的关系
在闭区间\([a,b]\)上的实值函数中,严格强弱递进关系为:
\[ \boxed{光滑(C^\infty)\subset 连续可导(C^1)\subset 可导 \subset 连续} \]\[ \boxed{Lipschitz连续 \subset 绝对连续 \subset 一致连续 \subset 连续} \]- 两类关系的唯一交集:可导且导数有界的函数同时属于\(C^1\)(若导数连续)和Lipschitz连续,是控制理论中最常用的函数类(如四旋翼线性化模型的状态方程);
- 无包含关系的核心边界:Lipschitz连续不蕴含可导(如\(|x|\)),可导不蕴含一致连续(如\(x^2\)在\(\mathbb{R}\)上);
- 应用优先级:轨迹规划优先选择光滑函数(保证高阶导数连续),非线性控制优先验证Lipschitz条件(保证稳定性),积分型Lyapunov函数需基于绝对连续函数构造。
1. 一致连续 ⊂ 连续(一致连续⇒连续,反之不真)
- 逻辑推导:一致连续的\(\delta\)不依赖于具体点\(x_0\),自然满足连续的“点态\(\delta\)”要求,故一致连续是更强的条件。
- 定理支撑:Heine-Cantor定理——闭区间\([a,b]\)上的连续函数必一致连续(此时二者等价);但开区间/无界区间上,连续≠一致连续。
- 反例(连续但不一致连续):\(f(x) = \frac{1}{x}\)在\((0,1)\)上连续。取\(\epsilon = 1\),对任意\(\delta > 0\),取\(x_1 = \frac{\delta}{2}\),\(x_2 = \frac{\delta}{4}\)(满足\(|x_1 - x_2| = \frac{\delta}{4} < \delta\)),但\(|f(x_1) - f(x_2)| = \frac{2}{\delta}\),当\(\delta < 2\)时,\(\frac{2}{\delta} > 1 = \epsilon\),故不一致连续。
- 控制理论应用:四旋翼轨迹规划中,若采用开区间定义的轨迹函数,需验证一致连续性以保证姿态平滑过渡。
2. 绝对连续 ⊂ 一致连续(绝对连续⇒一致连续,反之不真)
- 逻辑推导:绝对连续的条件包含“区间和可控性”,取单个区间\((x_1, x_2)\)时,即满足一致连续的定义,故绝对连续更强。
- 反例(一致连续但不绝对连续):Cantor函数\(C(x)\)(三分集上构造的单调不减函数)。其在\([0,1]\)上一致连续(单调有界函数必一致连续),但对任意\(\delta > 0\),可构造有限个互不重叠的区间,其长度和小于\(\delta\),但函数值差之和为1(超过任意\(\epsilon < 1\)),故不绝对连续。
- 控制理论应用:绝对连续保证Newton-Leibniz公式成立(\(f(x) = f(a) + \int_a^x f'(t)dt\)),是积分型Lyapunov函数设计的基础。
3. Lipschitz连续 ⊂ 绝对连续(Lipschitz连续⇒绝对连续,反之不真)
- 逻辑推导:设\(f\) Lipschitz连续(常数\(L\)),对任意\(\epsilon > 0\),取\(\delta = \frac{\epsilon}{L}\)。若\(\sum (y_i - x_i) < \delta\),则\(\sum |f(y_i) - f(x_i)| \leq L \sum (y_i - x_i) < L \cdot \frac{\epsilon}{L} = \epsilon\),满足绝对连续定义。
- 反例(绝对连续但非Lipschitz连续):\(f(x) = \sqrt{x}\)在\([0,1]\)上绝对连续。其导数\(f'(x) = \frac{1}{2\sqrt{x}}\)在\(x \to 0^+\)时无界,故不存在全局Lipschitz常数\(L\)(假设存在\(L\),则\(\frac{1}{2\sqrt{x}} \leq L\)对所有\(x \in (0,1]\)成立,矛盾)。
- 控制理论应用:Lipschitz条件是非线性系统(如四旋翼动力学模型)稳定性分析的核心假设,可通过Backstepping控制设计保证闭环系统鲁棒性。
4. 可导与连续性的关系:可导⇒连续,但与一致/绝对/Lipschitz连续无直接包含
- 逻辑推导:可导函数在导数存在点满足\(\lim_{x \to x_0} (f(x) - f(x_0)) = \lim_{x \to x_0} f'(x_0)(x - x_0) = 0\),故必连续;但可导不蕴含更强的连续性,更强的连续性也不蕴含可导。
- 反例1(Lipschitz连续但不可导):\(f(x) = |x|\)在\([-1,1]\)上Lipschitz连续(\(L=1\)),但在\(x=0\)处左导数为-1、右导数为1,导数不存在。
- 反例2(可导但非一致连续):\(f(x) = x^2\)在\(\mathbb{R}\)上可导(\(f'(x)=2x\)),但对\(\epsilon=1\),取\(x_1 = n\),\(x_2 = n + \frac{1}{2n}\)(\(n \in \mathbb{N}^+\)),则\(|x_1 - x_2| = \frac{1}{2n}\)可任意小,但\(|f(x_1) - f(x_2)| = 2n \cdot \frac{1}{2n} + (\frac{1}{2n})^2 = 1 + \frac{1}{4n^2} > \epsilon\),故不一致连续(更非Lipschitz连续)。
- 关键关联:仅当\(f\)可导且导数\(f'\)在\([a,b]\)上有界时,\(f\)才是Lipschitz连续(Lipschitz常数\(L = \sup_{x \in [a,b]} |f'(x)|\),由中值定理证明)。
- 控制理论应用:四旋翼控制器设计中,常假设动力学模型的非线性项满足Lipschitz条件,若模型可导且导数有界,可直接验证该条件。
5. 连续可导(\(C^1\))⊂ 可导(可导⇏连续可导)
- 逻辑推导:连续可导要求导数存在且连续,是可导的更强条件;可导函数的导数可能不连续。
- 反例(可导但非连续可导): \[ f(x) = \begin{cases} x^2 \sin\frac{1}{x}, & x \neq 0, \\ 0, & x = 0. \end{cases} \] 其导数为: \[ f'(x) = \begin{cases} 2x \sin\frac{1}{x} - \cos\frac{1}{x}, & x \neq 0, \\ 0, & x = 0. \end{cases} \] 当\(x \to 0\)时,\(\cos\frac{1}{x}\)震荡无极限,故\(f'(x)\)在\(x=0\)处不连续,\(f\)非\(C^1\)。
- 控制理论应用:\(C^1\)函数保证四旋翼轨迹的角速度连续,避免姿态突变导致的控制震荡。
6. 光滑(\(C^\infty\))⊂ 连续可导(\(C^1\))(\(C^1\)⇏\(C^\infty\))
- 逻辑推导:光滑函数要求任意阶导数存在且连续,是\(C^1\)的更强条件;\(C^1\)函数可能高阶不可导。
- 例子(\(C^1\)但非光滑):\(f(x) = |x|^3\)在\(\mathbb{R}\)上二阶可导(\(f''(x) = 6|x|\)),但三阶导数在\(x=0\)处不存在,故仅为\(C^2\),非\(C^\infty\)。
- 控制理论应用:光滑函数(如\(e^x\)、多项式轨迹)常用于四旋翼滑模控制的切换函数设计,可消除抖振。