在考虑非连续的向量场的时候,classical解具有非常大的局限性。 为了处理微分方程的不连续部分, 我们首先放宽解必须始终沿着向量场方向的要求。 数学中对应的就是绝对连续的Caratheodory解。
Caratheodory解不足以保证解的存在性。 由于向量场的非连续性, 他的值在任意靠近一个点的时候可能表现出显著的振荡。 这种不匹配可能导致无法构造一个Caratheodory解。
Filippov解的思路是不再只考虑向量场上的各个点, 而是考虑向量场上各个点邻域。其无法保证解的唯一性但是可以保证解的大多数性质。
本文序号和内容整理自:CORTES J. Discontinuous dynamical systems[J/OL]. IEEE Control Systems Magazine, 2008, 28(3): 36-73. DOI:10.1109/MCS.2008.919306.
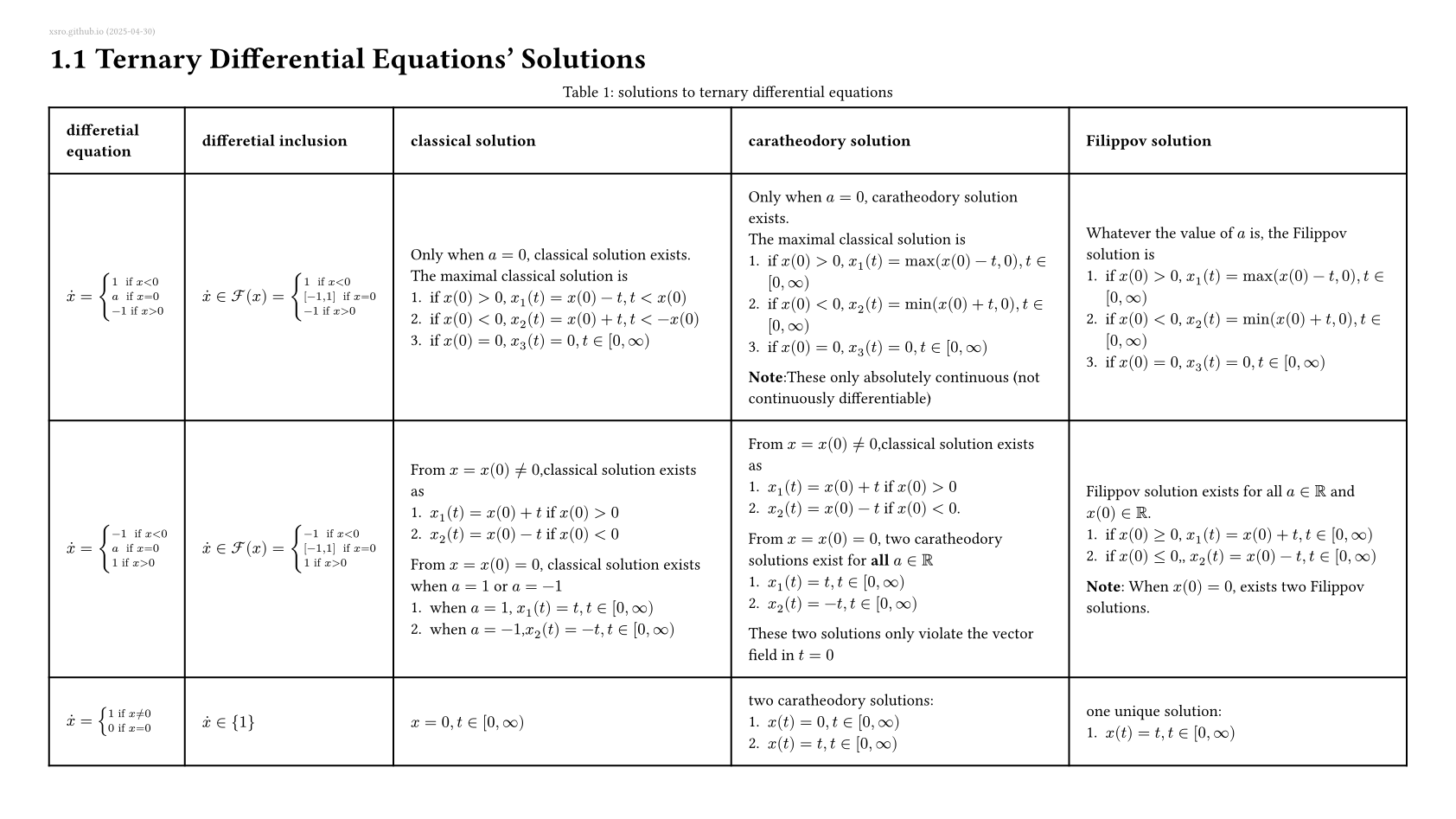
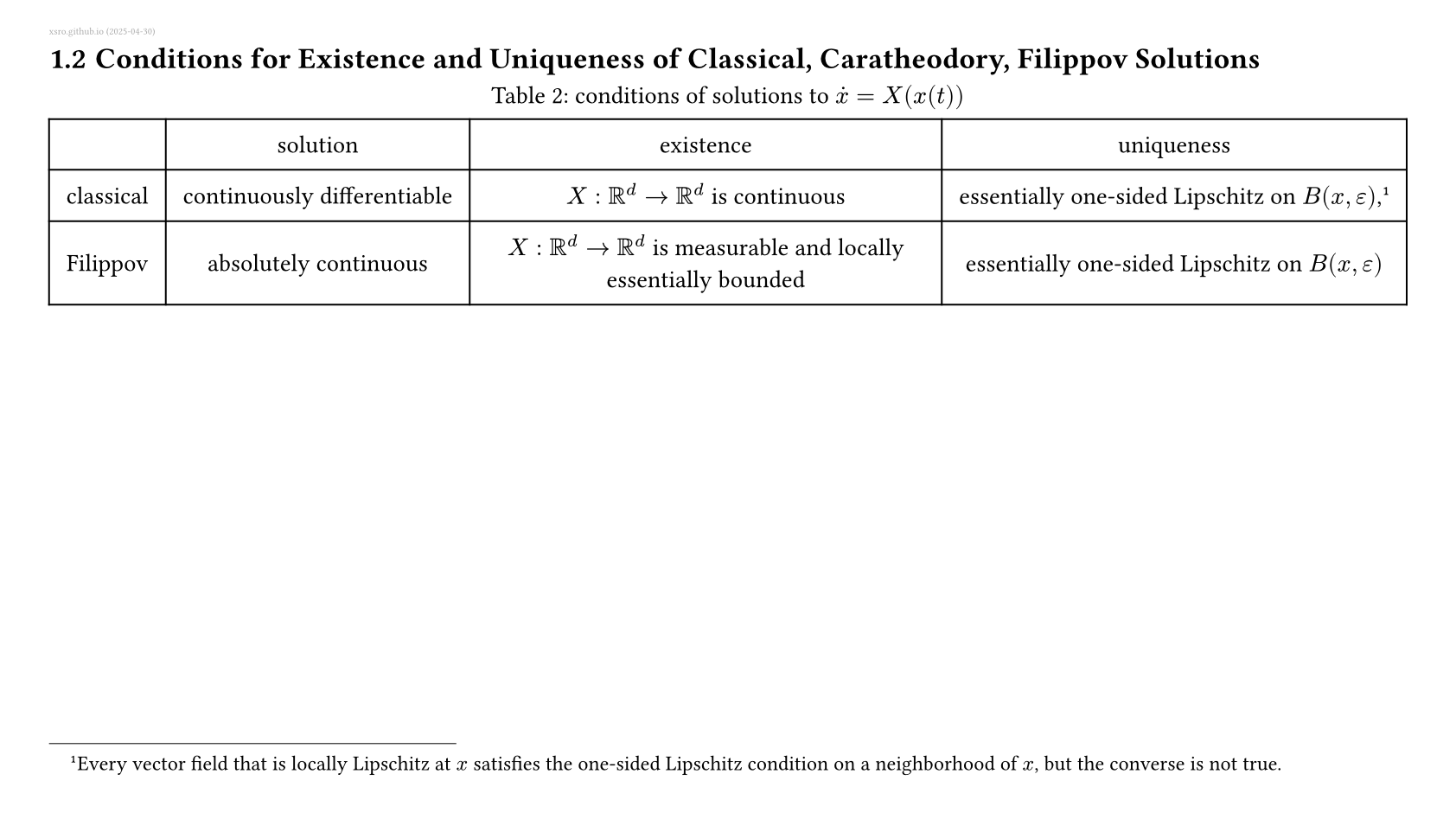
不一定连续可微的解
Beyond Continuously Differentiable Solutions
考虑如下的动态系统
$$ \dot{x}(t)=\mathcal{X}(x(t))\ x(t_0)=x_0 \tag{7} $$其中$x\in \mathbb{R}^d$, $d$为一个正整数, 并且$\mathcal{X}:\mathbb{R}^d \to \mathbb{R}^d$ 不需要连续。 我们称连续可微的解$t \mapsto x(t)$为经典(classical)解。 显然,如果$\mathcal{X}$连续,那么方程所有解都是classical的。 不失一般性,我们认为$t_0=0$,并且只考虑$t>0$的情况。
连续可微Continuously differentiable,用泛函表示就是函数$f\in C^1$,意味着函数的导数是连续的,当然可微保证其本身也是连续的。
Caratheodory解是classical解的一般化。 粗略地说,Caratheodory解是满足微分方程(7)的Lebesgue积分形式(8)的绝对连续曲线
$$ x(t)=x(t_0)+\int_{t_0}^t X(x(s)) ds,\quad t>t_0 \tag{8} $$通过使用积分形式(8),Caratheodory解不再要求方程解必须所有时间都沿着向量场的方向。 也就是说,微分方程(7)need bot be satisfied on a set of measure zero.
Filippov解使用微分包含式(differential inclusion)来替换微分方程(7)右侧
$$ \dot{x}(t)\in \mathcal{F} (x(t)) $$其中$\mathcal{F}:\mathbb{F}^d \to \mathfrak{B}(\mathbb{F}^d)$, $\mathfrak{B}(\mathbb{R}^d)$为d维实数空间$\mathbb{R}^d$的所有子集的集合。 Filippov解是绝对连续曲线。 对于任意给定的状态$x$,Filippov解不只关注向量场在$x$处的值, Filippov解的思想是引入由向量场中$x$的领域决定的一组方向集合。 文献中常常使用集值映射(set-value map), 也就是说这种映射的值是一个集合,而不像标准的函数(映射)的值只有一个。
An ordinary differential inclusion says the derivative must lie in a specified set, which may also depend on the function and independent variable.
Caratheodory解和Filippov解都不能完全解决非连续动态系统的问题, 围绕存在的问题由Sample-and-hold解以及其他的一些描述方法。
classical 解的存在性和唯一性
对于常微分方程而言,向量场如果只连续不能保证解的唯一性。 我们说解的一个性质弱,表示不是所有解满足这一性质。 我们说解的一个性质强,表示所有解满足这一性质。 所以设计控制器的思路可以是
- 设计控制器并考虑控制器下的闭环系统
- 用一个集值映射将每一个状态映射到允许的输入产生的所有向量的集合,并将这个映射与控制系统关联起来,(原文表述如下)
associate with the control system the set-valued map that assigns each state to the set of all vectors generated by the allowable inputs and consider the resulting differential inclusion.
classical 解的存在性
考虑微分方程:
$$ \dot{x}(t)=X(x(t)),\quad x(0)=x_0 \tag{10} $$其中$X:\mathbb{R}^d \to \mathbb{R}^d$是一个向量场。 如果$0=X(x_e)$,那么点$x_e\in \mathbb{R}^d$是(10)的一个平衡点。 在$[0,t_1]$上一个(10)的classical解是一个连续可微的映射$x:[0,t_1]\to\mathbb{R}^d$。 不失一般性,我们只考虑从时间$t_0=0$开始的解。 如果解$t\mapsto x(t)$ 不能在时间上延申(extend), 也就是说解不是定义域内更大的一个时间区间上的解的截断, 那么称该解为最大解(maximal solution)。 最大解的定义暗示了解的区间只能是$[0,T),T>0$或$[0,\infty)$。
Peano’s theorem 说明了连续的向量场可以保证classical解存在:
(Proposition 1) 令$X:\mathbb{R}^d\to \mathbb{R}^d$是连续向量场。 于是,对于所有$x_0\in\mathbb{R}^d$, 存在一个(10)的classical解,该解满足$x(0)=x_0$
classical 解的唯一性
(Proposition 2) 令$x:\mathbb{R}^d\to\mathbb{R}^d$连续, 假设对于所有的$x\in\mathbb{R}^d$, 存在一个$\epsilon>0$使得$X$是在状态$x$的$\epsilon$领域$B(x,\epsilon)$上单侧Lipschitz连续。 然后,对于所有$x_0\in \mathbb{R}^d$,存在一个起始于$x(0)=x_0$的(10)的唯一的classical 解
classical 解存在性和唯一性示例
下面的例子说明如果向量场不连续,那么(10)可能不存在经典解
考虑如下向量场:$X:\mathbb{R}\to\mathbb{R}$
$$ X(x)=\begin{cases} -1, & x>0\\ 1 , & x\leq 0 \end{cases} $$显然在$x=0$处该函数不连续。 假设存在一个连续可微的解满足$\dot{x}(t)=X(x(t))$和$x(0)=0$。 然后$\dot{x}(0)=X(x(0))=X(0)=1$, 于是,对于所有的充分小的时间$t$,$x(t)>0$ 并且$\dot{x}(t)=X(x(t))=-1$, 这与$t\mapsto \dot{x}(t)$连续矛盾。 所以,不存在classical 解。
下面的例子说明如果向量场不连续,那么(10)也可能存在经典解。
考虑向量场$X:\mathbb{R}\to\mathbb{R}$
$$ X(x)=-\mathrm{sign}(x)=\begin{cases} -1, & x>0,\\ 0, & x=0,\\ 1, & x<0, \end{cases} $$唯一最大解为:
$$ \begin{aligned} &x(t)=x(0)-t, t\in [0,x(0)) &\textrm{if} \ x(0)>0, \\ &x(t)=0, t\in [0,\infty) &\textrm{if}\ x(0)=0 \\ &x(t)=x(0)+t, t\in [0,-x(0)) &\textrm{if}\ x(0)<0, \end{aligned} $$
下面例子说明连续但是不是单侧Lipschitz连续的向量场可能有多个classical解
考虑向量场$X:\mathbb{R}\to\mathbb{R}$
$$ X(s)=\sqrt{|x|} $$这个向量场处处连续,并在$\mathbb{R}/\{0\}$局部Lipschitz连续, 但是在零处不局部连续,在零的领域也不单侧Lipschitz连续。 从$x(0)=0$开始,该动态系统有许多最大解,具体而言为: 对所有$a>0$,$x_a:[0,\infty)\to \mathbb{R}$,表达式为:
$$ x_a(t)=\begin{cases} 0, & 0\leq t \leq a,\\ (t-a)^2/4, & t\geq a \end{cases} $$
下面例子说明连续但是不是单侧Lipschitz连续的向量场只有一个classical解
考虑向量场$X:\mathbb{R}\to\mathbb{R}$
$$ X(s)=\begin{cases} -x \mathrm{log} x, & x>0\\ 0, & x=0,\\ x \mathrm{log}(-x),& x<0, \end{cases} $$唯一最大解为:
$$ \begin{aligned} &x(t)=-\exp(\log (-x(0)) \exp(t)), &\textrm{if}\ x(0)<0 \\ &x(t)=0, &\textrm{if}\ x(0)=0 \\ &x(t)=\exp(\log x(0) \exp(-t)), &\textrm{if}\ x(0)>0 \end{aligned} $$
Caratheodory解
数学定义
考虑微分方程:
$$ \dot{x}(t)=X(x(t)),\quad x(0)=x_0. \tag{10} $$微分方程(10) 的定义在$[0,t_1]\subset \mathbb{R}$的Caratheodory解是一个绝对连续映射。 该映射在几乎(almost)所有时间$t\in [0,t_1]$上满足微分方程(10)。 这里说的“几乎”是在Lebesgue测度的意义上的。 也就是说,Caratheodory解只在Lebesgue测度为0的时刻集合上没有沿着向量场的方向。 也可以等价地说,Caratheodory解是满足微分方程(10)的Lebesgue积分形式(16)的绝对连续解。
$$ x(t)=x(t_0)+\int_{t_0}^t X(x(s)) ds,\quad t>t_0 \tag{16} $$当然,所有的classical解都是Caratheodory解。
Example 9: 具有Caratheodory解,但是没有classical 解的系统
$$ X(x)=\begin{cases} 1, & x>0,\\ \frac{1}{2}, & x=0,\\ -1, & x<0\\ \end{cases} $$该系统由两个从$x(0)=0$出发的Caratheodory解,分别是 $x_1(t)=t,t\in [0,\infty)$和$x_1(t)=-t,t\in [0,\infty)$。 这两个解在$t=0$时,都不满足向量场,也就是 $\dot{x}_1(0) \neq X(x_1(0))$ 和 $\dot{x}_2(0) \neq X(x_2(0))$ 。
然而,可以找到很多不接受Caratheodory解的系统,这其中一些可以用Filippov解理解。
Example 9: 不具有Caratheodory解的系统
$$ X(x)=\begin{cases} -1, & x\geq 0,\\ 1, & x<0\\ \end{cases} $$该系统的解会沿着$x=0$处反复振荡,所以不具有Caratheodory解,而需要使用Filippov解
Caratheodory解存在的充分性条件
对于时变的向量场,Caratheodory解存在的条件应用到时不变系统与classical解类似。 所以研究主要集中在时不变的向量场,如directionally continuous 和 Patchy vector fields, 详情参看原文。
微分包含的Caratheodory解
数学分析中的微分包含式(Differential inclusion)是指具有如下形式的常微分方程式:
$$ \dot{x}(t)\in \mathcal{F}(t,x(t)) \tag{S2} $$其中$\mathcal{F}(t,x(t))$表示一个集合,而非$\mathbb{R}^d$空间中的一个点。 而映射$\mathcal{F}: [0,\infty)\times \mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$称为集值映射(set-valued map)。
集值映射的有界性
如果存在 $\epsilon,\delta \in (0,\infty)$ 和一个可积函数 $m:[t,t+\delta]\to (0,\infty)$ 使得 $\Vert z \Vert_2\leq m(s)$ 对所有的 $z\in \mathcal{F}(s,y)$、 所有的 $s\in [t,t+t+\delta]$ 和所有的$y\in B(x,\epsilon)$ 成立, 那么称集值映射 $\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$ 在 $(t,x)\in [0,\infty)\times \mathbb{R}^d$ 局部有界(locally bounded)。
如果存在 $\epsilon,\delta \in (0,\infty)$ 和一个可积函数 $m:[t,t+\delta]\to (0,\infty)$ 使得 $\Vert z \Vert_2\leq m(s)$ 对所有的 $z\in \mathcal{F}(s,y)$、 所有的 $s\in [t,t+t+\delta]$ 和几乎所有的$y\in B(x,\epsilon)$ 在Lebesgue测度意义上成立, 那么称集值映射 $\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$ 在 $(t,x)\in [0,\infty)\times \mathbb{R}^d$ 局部本性有界(locally essentially bounded)。
集值映射的连续性
- 如果对于任意$\epsilon \in (0,\infty)$,存在$\delta \in (0,\infty)$使得$\mathcal{F}(y) \subseteq \mathcal{F}(x)+B(0,\epsilon)$对所有$y\in B(x,\delta)$成立,那么称集值映射$\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$是上半连续的。
- 如果对于任意$\epsilon \in (0,\infty)$,存在$\delta \in (0,\infty)$使得$\mathcal{F}(x) \subseteq \mathcal{F}(y)+B(0,\epsilon)$对所有$y\in B(x,\delta)$成立,那么称集值映射$\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$是下半连续的。
- 如果集值映射$\mathcal{F}:\mathbb{R}^d\to\mathfrak(\mathbb{R}^d)$ 在$x\in \mathbb{R}^d$既是上半连续和下半连续的,那么称其在$x\in \mathbb{R}^d$连续的。
最后,如果存在一个常数$L_x$以及$\epsilon\in (0,\infty)$使得
$$ \mathcal{F}(y')\subseteq \mathcal{F}(y) +L_x \Vert y-y'\Vert_2 \overline{B}(0,1) $$对所有$y,y' \in B(x,\epsilon)$成立, 那么称集值映射$\mathcal{F}:\mathbb{R}^d\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$局部Lipschitz连续。 在$x\in \mathbb{R}^d$局部Lipschitz连续的集值映射是上半连续的,反之不成立。
微分包含的Caratheodory解
如果$0\in \mathcal{F}(t,x_e)$对所有的$t\in [0,\infty)$成立, 那么称点$x_e\in \mathbb{R}^d$是微分包含的平衡点。 微分包含(S2)定义在$[t_0,t_1]\subset [0,\infty)$ 的caratheodory解是一个在$t\in [t_0,t_1]$上几乎处处满足$\dot{x}(t)\in \mathcal{F}(t,x(t))$的绝对可微的映射。
Proposition S2 微分包含的 caratheodory 解存在性定理 令集值映射$\mathcal{F}: [0,\infty)\times \mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$为一个局部有界的非空凸紧集。 假设,对于每一个$t\in \mathbb{R}$,集值映射$x\mapsto \mathcal{F}(t,x)$是上半连续的(upper-semicontinuous)。 然后,对于所有的$(t_0,x_0)\in [0,\infty)\times \mathbb{R}^d$, 存在一个初值为$x(t_0)=x_0$的caratheodory解
Proposition S3 在Proposition S2的基础上,假设,对所有的$x\in \mathbb{R}^d$,存在$\epsilon \in (0,\infty)$和一个积分函数$L_x: \mathbb{R}\to (0,\infty)$使得
$$ (v-w)^T(y-y')\leq L_x(t) \Vert y-y'\Vert^2_2, $$对几乎所有$y,y'\in B(x,\epsilon)$和所有$t\in [0,\infty)$,所有$v\in \mathcal{F}(t,y)$和所有$w\in \mathcal{F}(t,y')$
以下的集值映射是上半连续的,但是不是下半连续的,也就是说不是连续的, 因此他满足caratheodory解的存在性条件。 由于$y$和$y'$非零,$\mathcal{F}$满足caratheodory解的唯一性条件。
$$ \mathcal{F}(x)=\begin{cases} 0, & x\neq 0,\\ [-1,1], &x=0 \end{cases} $$Filippov解
Filippov解使用集值映射来替换原来的系统的右侧方程。 微分方程的 Filippov 解就是用Filippov集值映射替换微分方程右侧后得到的微分包含的 Caratheodory 解。 但是Caratheodory解和Filippov解总体上并没有什么关系
Filippov解的数学定义
令$\mathfrak{B}(\mathbb{R}^d)$表示$\mathbb{R}^d$中的所有子集的集合。 对于映射$X:\mathbb{R}^d\to \mathbb{R}^d$,定义Filippov集值映射(Filippov set-valued map)$F[X]:\mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$为
$$ F[X](x)\triangleq \bigcap_{\delta > 0} \bigcap_{\mu(S)=0} \overline{\mathrm{co}} \{X(B(x,\delta) \backslash S)\} \tag{19} $$这里的$\overline{\mathrm{co}}$表示凸包(convex closure), 这里的$\backslash$运算符,是集合的补集,$B\backslash A =B\cap A^C=\{x\in B | x\notin A\}$, 这里的$\mu$表示Lebesgue测度。 根据Filippov集值映射的定义,$F[X]$在点$x$的值$F[X](x)$与向量场$X$在$x$的值$X(x)$无关(由$x$领域上值决定)。
于是微分方程(10) $\dot{x}=X(x(t))$可以使用如下的微分包含(differential inclusion)表示
$$ \dot{x}(t)\in F[X](x(t)). \tag{21} $$微分方程(10)在$[0,t_1]\subset \mathbb{R}$的Filippov解 是几户满足所有时间$t\in [0,t_1]$的(21)的绝对连续解。 等价地,(10)的一个Filippov解是微分包含(21)的一个Caratheodory解。
微分包含(21)如果满足以下两个条件那么称为Filippov微分包含(Filippov DI)
- $F[X](x(t))\subset T_x \mathbb{R}^d$ 对于任意$x$是非空紧凸集(non-empty, compact and convex for any x), $ T_x\mathbb{R}^d$为切空间;
- 映射$F[X]$是上半连续集值映射(upper-semicontinuous set function):如果$x\to y$,集合$F[X](x)$中的间与$F[X](y)$中的点距离趋于零
Filippov解的存在性
Proposition 3 令$X:\mathbb{R}^d\to\mathbb{R}^d$是一个可测的、局部本性有界的映射。 然后,对于所有$x_0\in \mathbb{R}^d$,存在一个从$x(0)=x_0$开始的(10)的Filippov解。
这里局部本性有界(locally essentially bounded)指在每个点的有界邻域上都有界,这里的邻域要排除测度为零的集合。 该条件等价于微分包含的caratheodory解条件。 也就是说满足该条件的微分方程可以通过(19)转换为Filippov微分包含。