The map of Control Theory v5 简析
学习控制理论可以说经常可以看到Brian Douglas的The Map of Control Theory ,如下图所示。在感慨控制理论的博大精深的同时,我也想试着了解一下具体都是哪些内容。其中大部分内容我还没有学过,所以不一定对,仅供参考。
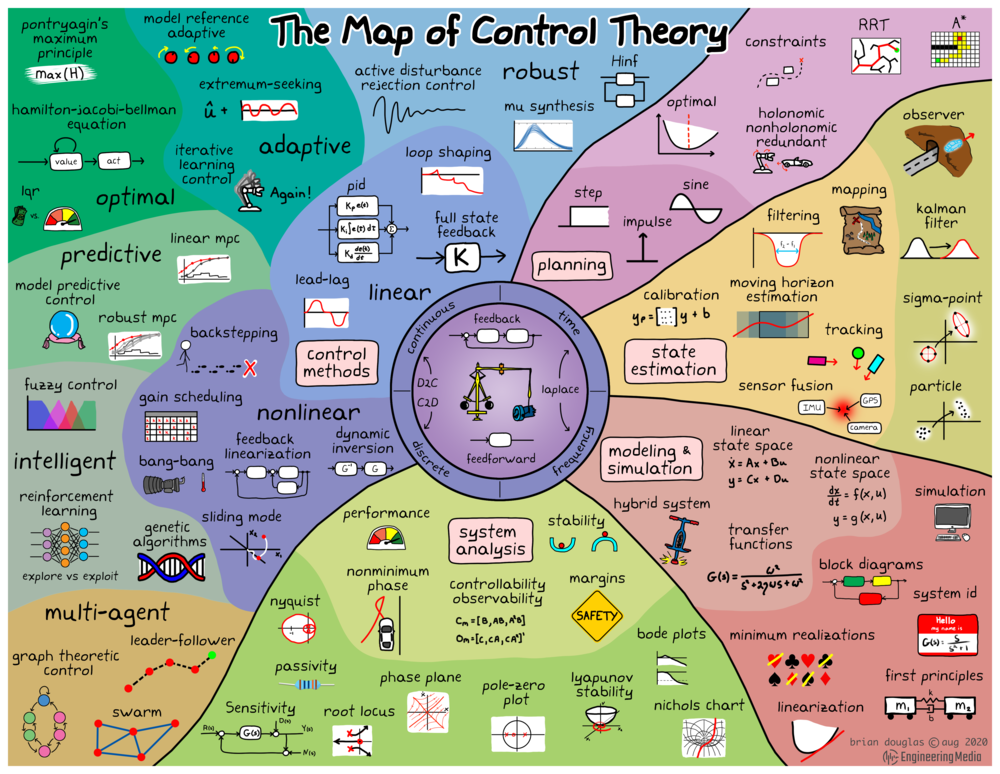
可以看出 map 包括一个圆和周边的 5 个区域,五个区域分别为
- 建模与仿真(modeling & simulation)
- 系统分析(system analysis)
- 控制方法(control methods)
- 规划(planning)
- 状态估计(state estimation)
位于中心的圆
首先,看图片中心的圆,
- 圆的中心是可以视为控制理论起源的离心式调速器(centrifugal governor,又称瓦特调速器或飞球调速器)
- 调速器上方是经典的反馈控制系统(又叫闭环控制系统),下方是前馈控制器。
- 圆周左半边是连续(continuous)控制系统和离散(discrete)控制系统,
- D2C 即离散系统转化为连续系统,通常使用保持器
- C2D 即连续系统转化为离散系统,通常使用采样器
- 圆周右半边,是分析控制系统的域(domain)
- 右上为时间域(time)
- 右下为频率域(frequency)(严格来说,应该叫复频域)
- 两者之间可以通过拉普拉斯变换(Laplace Transform)进行转化
建模与仿真
位于右下角的是建模与仿真模块(modeling & simulation),这里讨论如何对控制系统建立模型(通常为数学模型)并进行仿真。
经典控制理论中的数学模型通常为传递函数(transfer function)。现代控制理论中有线性状态空间(linear state space)方程,以及非线性状态空间(nonlinear state space)方程,可以从表达式中看出,非线性的状态空间方程右侧无法用线性函数表示出来。
此外还有混杂系统(hybrid system),通常指同时包含连续和离散动态特性的系统。
在仿真(simulation)部分,有方框图(block diagrams)、
- 系统辨识(system id or system identification):根据输入输出数据辨识出系统的表达式
- 最小实现(minimum realization or minimal realization):用状态最少的状态空间方程来实现传递函数,使得输入输出关系相同
- 线性化(linearization):模型线性化
- First principles:这个我不懂,应该就是指机理建模,或者叫做分析法建模,与之相对应的是实验法建模
系统分析
位于正下方的是控制系统分析(system analysis)部分,控制系统可以从下列角度分析
- 性能(performance)指标:动态性能指标和静态性能指标
- 是不是非最小相位(nonminimum phase)
- 系统稳定性(stability)
- 稳定裕度(margin)
- 可控性和可观性(controllability and observability)
- 李雅普诺夫稳定(lyapunov stability)
- 无源性(passivity):图中画了一个无源元件:电阻
- 敏感性(sensitivity):是研究数学模型或系统(数值或其他)输出中的不确定性如何在其输入中被分配到不同的不确定性来源
此外还可以借助图示法来进行分析:
- 零极点图(pole-zero plot)
- 根轨迹图(root locus plot)
- 伯德图(bode plot,对数频率特性曲线)
- 奈奎斯特图(nyquist plot,幅相频率特性图,幅相图)
- 尼科尔斯图(nichols plot,对数福相曲线)
- 相平面(phase plane):主要用来研究非线性系统
状态估计
位于右侧的是状态估计(state estimation)部分,通过各种方式估计系统通常无法直接测量的内部状态。
- 校准(calibration)
- 滤波(filtering)
- 滚动时域估计(HME,moving horizon estimation)
- 传感器融合(Sensor fusion)
- 跟踪(tracking)
- 制图(mapping)
- 观测器(observer)
- 卡尔曼滤波(kalman filter)
- Sigma 点(Sigma-point)
- 粒子滤波(Particle)
规划
位于右上方的是路径规划(Planning)部分,研究如何规划路线(path)
- 阶跃(step)
- 冲激(impulse)
- 正弦(sine)
- 最优(optimal)
- 约束(constraints)
- 完整冗余/非完整冗余(holonomic/nonholonomic redundant)
- 基于快速扩展随机树(rapidly exploring random tree,RRT)
- A*
控制方法
整个左上部分都是关于控制方法的,这也是控制理论的最重大的部分。不同的目的,不同的对象使用不同的控制方法
线性控制 Linear
- 回路成形(loop shaping)
- 比例-积分-微分(PID,proportional–integral–derivativel)控制
- 全状态反馈(Full state feedback)
- 超前-滞后(Lead-lag)校正
非线性控制 Nonlinear
- 反推控制(backstepping)
- 增益调度(gain scheduling)
- bang-bang控制(bang-bang control)
- 回授线性化Feedback linearization)
- 滑模控制(sliding mode,滑动模态控制)
- dynamic inversion
预测控制 Predictive
- 模型预测控制(model predictive control, MPC)
- 鲁棒预测控制(Robust MPC)
- 线性预测控制(Linear MPC)
最优控制 Optimal
- 庞特里亚金最大化原理(pontryagin’s maximum principle)
- 哈密顿-雅可比-贝尔曼方程(Hamilton-jacobi-bellman equation)
- 线性二次型控制(LQR, linear–quadratic regulator)
自适应控制 Adaptive
- 模型参考自适应(model reference adaptive)
- 极值搜索(Extremum-seeking)
- 迭代学习控制(Iterative learning control)
鲁棒控制 Robust
- 自抗扰控制(active disturbance rejection control, ADRC)
- mu synthesis, $\mu$ Synthesis
- H 无穷(H-infinity method, $H_\infty$)
智能控制 Intelligent
- 模糊控制(fuzzy control)
- 强化学习(reinforcement learning)
- 遗传算法(genetic algorithms)
多智能体 Multi-agent
- 基于图理论的控制(graph theoretic control)
- 领导者-跟随者(Leader-follower)
- 蜂群(Swarm)控制