前文已经说明了在考虑非连续的向量场的时候,classical解具有非常大的局限性。 为了处理微分方程的不连续部分, 我们首先放宽解必须始终沿着向量场方向的要求。 数学中对应的就是绝对连续的Caratheodory解。
Caratheodory解不足以保证解的存在性。 由于向量场的非连续性, 他的值在任意靠近一个点的时候可能表现出显著的振荡。 这种不匹配可能导致无法构造一个Caratheodory解。
Filippov解的思路是不再只考虑向量场上的各个点, 而是考虑向量场上各个点邻域。
Caratheodory解
数学定义
考虑微分方程:
$$ \dot{x}(t)=X(x(t)),\quad x(0)=x_0. \tag{10} $$微分方程(10) 的定义在$[0,t_1]\subset \mathbb{R}$的Caratheodory解是一个绝对连续映射。 该映射在几乎(almost)所有时间$t\in [0,t_1]$上满足微分方程(10)。 这里说的“几乎”是在Lebesgue测度的意义上的。 也就是说,Caratheodory解只在Lebesgue测度为0的时刻集合上没有沿着向量场的方向。 也可以等价地说,Caratheodory解是满足微分方程(10)的Lebesgue积分形式(16)的绝对连续解。
$$ x(t)=x(t_0)+\int_{t_0}^t X(x(s)) ds,\quad t>t_0 \tag{16} $$当然,所有的classical解都是Caratheodory解。
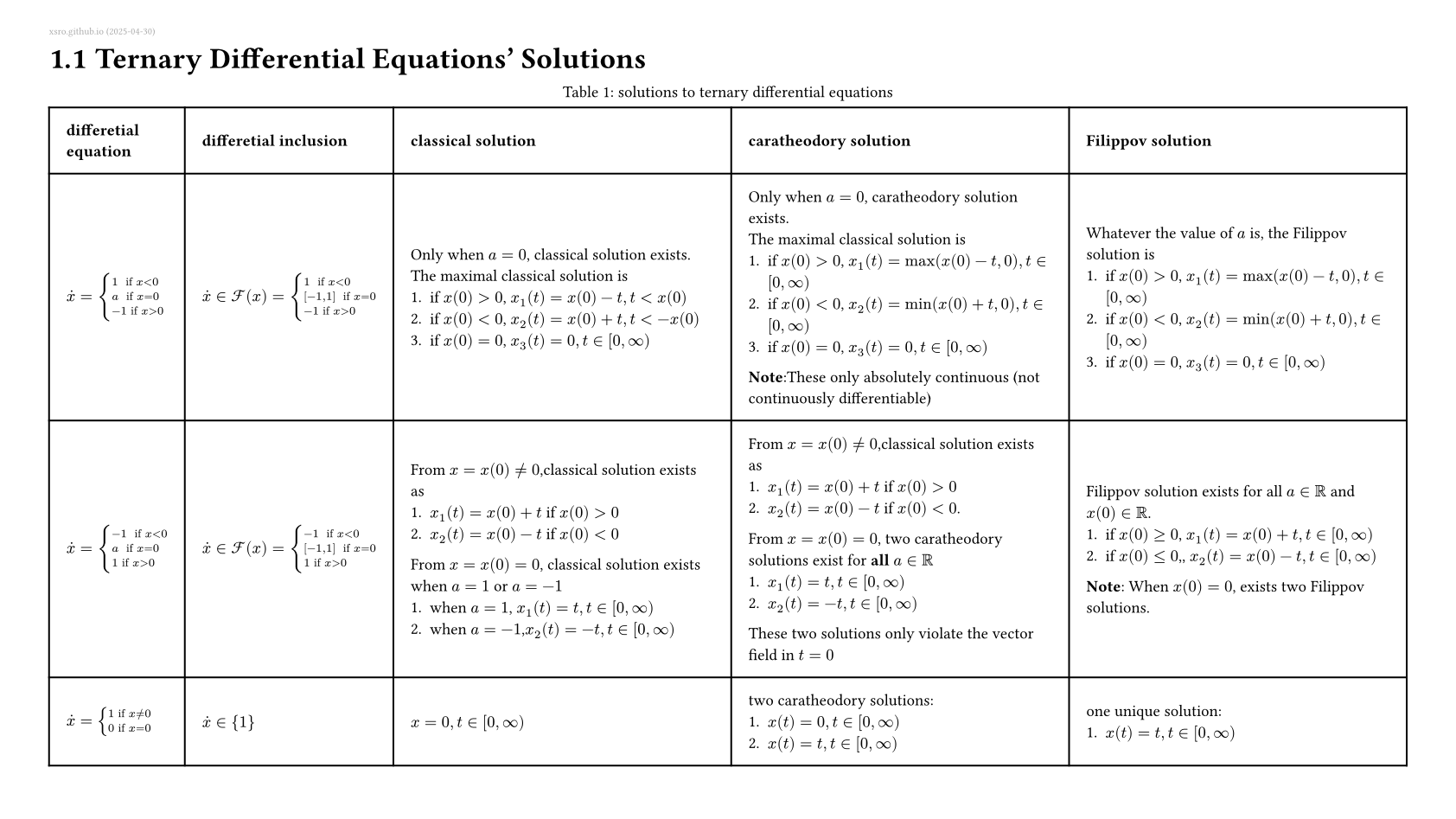
Example 9: 具有Caratheodory解,但是没有classical 解的系统
$$ X(x)=\begin{cases} 1, & x>0,\\ \frac{1}{2}, & x=0,\\ -1, & x<0\\ \end{cases} $$该系统由两个从$x(0)=0$出发的Caratheodory解,分别是 $x_1(t)=t,t\in [0,\infty)$和$x_1(t)=-t,t\in [0,\infty)$。 这两个解在$t=0$时,都不满足向量场,也就是 $\dot{x}_1(0) \neq X(x_1(0))$ 和 $\dot{x}_2(0) \neq X(x_2(0))$ 。
然而,可以找到很多不接受Caratheodory解的系统,这其中一些可以用Filippov解理解。
Example 9: 不具有Caratheodory解的系统
$$ X(x)=\begin{cases} -1, & x\geq 0,\\ 1, & x<0\\ \end{cases} $$该系统的解会沿着$x=0$处反复振荡,所以不具有Caratheodory解,而需要使用Filippov解
Caratheodory解存在的充分性条件
对于时变的向量场,Caratheodory解存在的条件应用到时不变系统与classical解类似。 所以研究主要集中在时不变的向量场,如directionally continuous 和 Patchy vector fields, 详情参看原文。
微分包含的Caratheodory解
数学分析中的微分包含式(Differential inclusion)是指具有如下形式的常微分方程式:
$$ \dot{x}(t)\in \mathcal{F}(t,x(t)) \tag{S2} $$其中$\mathcal{F}(t,x(t))$表示一个集合,而非$\mathbb{R}^d$空间中的一个点。 而映射$\mathcal{F}: [0,\infty)\times \mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$称为集值映射(set-valued map)。
集值映射的有界性
如果存在 $\epsilon,\delta \in (0,\infty)$ 和一个可积函数 $m:[t,t+\delta]\to (0,\infty)$ 使得 $\Vert z \Vert_2\leq m(s)$ 对所有的 $z\in \mathcal{F}(s,y)$、 所有的 $s\in [t,t+t+\delta]$ 和所有的$y\in B(x,\epsilon)$ 成立, 那么称集值映射 $\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$ 在 $(t,x)\in [0,\infty)\times \mathbb{R}^d$ 局部有界(locally bounded)。
如果存在 $\epsilon,\delta \in (0,\infty)$ 和一个可积函数 $m:[t,t+\delta]\to (0,\infty)$ 使得 $\Vert z \Vert_2\leq m(s)$ 对所有的 $z\in \mathcal{F}(s,y)$、 所有的 $s\in [t,t+t+\delta]$ 和几乎所有的$y\in B(x,\epsilon)$ 在Lebesgue测度意义上成立, 那么称集值映射 $\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$ 在 $(t,x)\in [0,\infty)\times \mathbb{R}^d$ 局部本性有界(locally essentially bounded)。
集值映射的连续性
- 如果对于任意$\epsilon \in (0,\infty)$,存在$\delta \in (0,\infty)$使得$\mathcal{F}(y) \subseteq \mathcal{F}(x)+B(0,\epsilon)$对所有$y\in B(x,\delta)$成立,那么称集值映射$\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$是上半连续的。
- 如果对于任意$\epsilon \in (0,\infty)$,存在$\delta \in (0,\infty)$使得$\mathcal{F}(x) \subseteq \mathcal{F}(y)+B(0,\epsilon)$对所有$y\in B(x,\delta)$成立,那么称集值映射$\mathcal{F}:[0,\infty)\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$是下半连续的。
- 如果集值映射$\mathcal{F}:\mathbb{R}^d\to\mathfrak(\mathbb{R}^d)$ 在$x\in \mathbb{R}^d$既是上半连续和下半连续的,那么称其在$x\in \mathbb{R}^d$连续的。
最后,如果存在一个常数$L_x$以及$\epsilon\in (0,\infty)$使得
$$ \mathcal{F}(y')\subseteq \mathcal{F}(y) +L_x \Vert y-y'\Vert_2 \overline{B}(0,1) $$对所有$y,y’ \in B(x,\epsilon)$成立, 那么称集值映射$\mathcal{F}:\mathbb{R}^d\to \mathfrak{B}(\mathbb{R}^d)$在$x\in \mathbb{R}^d$局部Lipschitz连续。 在$x\in \mathbb{R}^d$局部Lipschitz连续的集值映射是上半连续的,反之不成立。
微分包含的Caratheodory解
如果$0\in \mathcal{F}(t,x_e)$对所有的$t\in [0,\infty)$成立, 那么称点$x_e\in \mathbb{R}^d$是微分包含的平衡点。 微分包含(S2)定义在$[t_0,t_1]\subset [0,\infty)$ 的caratheodory解是一个在$t\in [t_0,t_1]$上几乎处处满足$\dot{x}(t)\in \mathcal{F}(t,x(t))$的绝对可微的映射。
Proposition S2 微分包含的 caratheodory 解存在性定理 令集值映射$\mathcal{F}: [0,\infty)\times \mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$为一个局部有界的非空凸紧集。 假设,对于每一个$t\in \mathbb{R}$,集值映射$x\mapsto \mathcal{F}(t,x)$是上半连续的(upper-semicontinuous)。 然后,对于所有的$(t_0,x_0)\in [0,\infty)\times \mathbb{R}^d$, 存在一个初值为$x(t_0)=x_0$的caratheodory解
Proposition S3 在Proposition S2的基础上,假设,对所有的$x\in \mathbb{R}^d$,存在$\epsilon \in (0,\infty)$和一个积分函数$L_x: \mathbb{R}\to (0,\infty)$使得
$$ (v-w)^T(y-y')\leq L_x(t) \Vert y-y'\Vert^2_2, $$对几乎所有$y,y’\in B(x,\epsilon)$和所有$t\in [0,\infty)$,所有$v\in \mathcal{F}(t,y)$和所有$w\in \mathcal{F}(t,y’)$
以下的集值映射是上半连续的,但是不是下半连续的,也就是说不是连续的, 因此他满足caratheodory解的存在性条件。 由于$y$和$y’$非零,$\mathcal{F}$满足caratheodory解的唯一性条件。
$$ \mathcal{F}(x)=\begin{cases} 0, & x\neq 0,\\ [-1,1], &x=0 \end{cases} $$Filippov解
Filippov解使用集值映射来替换原来的系统的右侧方程。 微分方程的 Filippov 解就是用Filippov集值映射替换微分方程右侧后得到的微分包含的 Caratheodory 解。 但是Caratheodory解和Filippov解总体上并没有什么关系
Filippov解的数学定义
令$\mathfrak{B}(\mathbb{R}^d)$表示$\mathbb{R}^d$中的所有子集的集合。 对于映射$X:\mathbb{R}^d\to \mathbb{R}^d$,定义Filippov集值映射(Filippov set-valued map)$F[X]:\mathbb{R}^d \to \mathfrak{B}(\mathbb{R}^d)$为
$$ F[X](x)\triangleq \bigcap_{\delta > 0} \bigcap_{\mu(S)=0} \overline{\mathrm{co}} \{X(B(x,\delta) \backslash S)\} \tag{19} $$这里的$\overline{\mathrm{co}}$表示凸包(convex closure), 这里的$\backslash$运算符,是集合的补集,$B\backslash A =B\cap A^C={x\in B | x\notin A}$, 这里的$\mu$表示Lebesgue测度。 根据Filippov集值映射的定义,$F[X]$在点$x$的值$FX$与向量场$X$在$x$的值$X(x)$无关(由$x$领域上值决定)。
于是微分方程(10) $\dot{x}=X(x(t))$可以使用如下的微分包含(differential inclusion)表示
$$ \dot{x}(t)\in F[X](x(t)). \tag{21} $$微分方程(10)在$[0,t_1]\subset \mathbb{R}$的Filippov解 是几户满足所有时间$t\in [0,t_1]$的(21)的绝对连续解。 等价地,(10)的一个Filippov解是微分包含(21)的一个Caratheodory解。
微分包含(21)如果满足以下两个条件那么称为Filippov微分包含(Filippov DI)
- $FX\subset T_x \mathbb{R}^d$ 对于任意$x$是非空紧凸集(non-empty, compact and convex for any x), $ T_x\mathbb{R}^d$为切空间;
- 映射$F[X]$是上半连续集值映射(upper-semicontinuous set function):如果$x\to y$,集合$FX$中的间与$FX$中的点距离趋于零
Filippov解的存在性
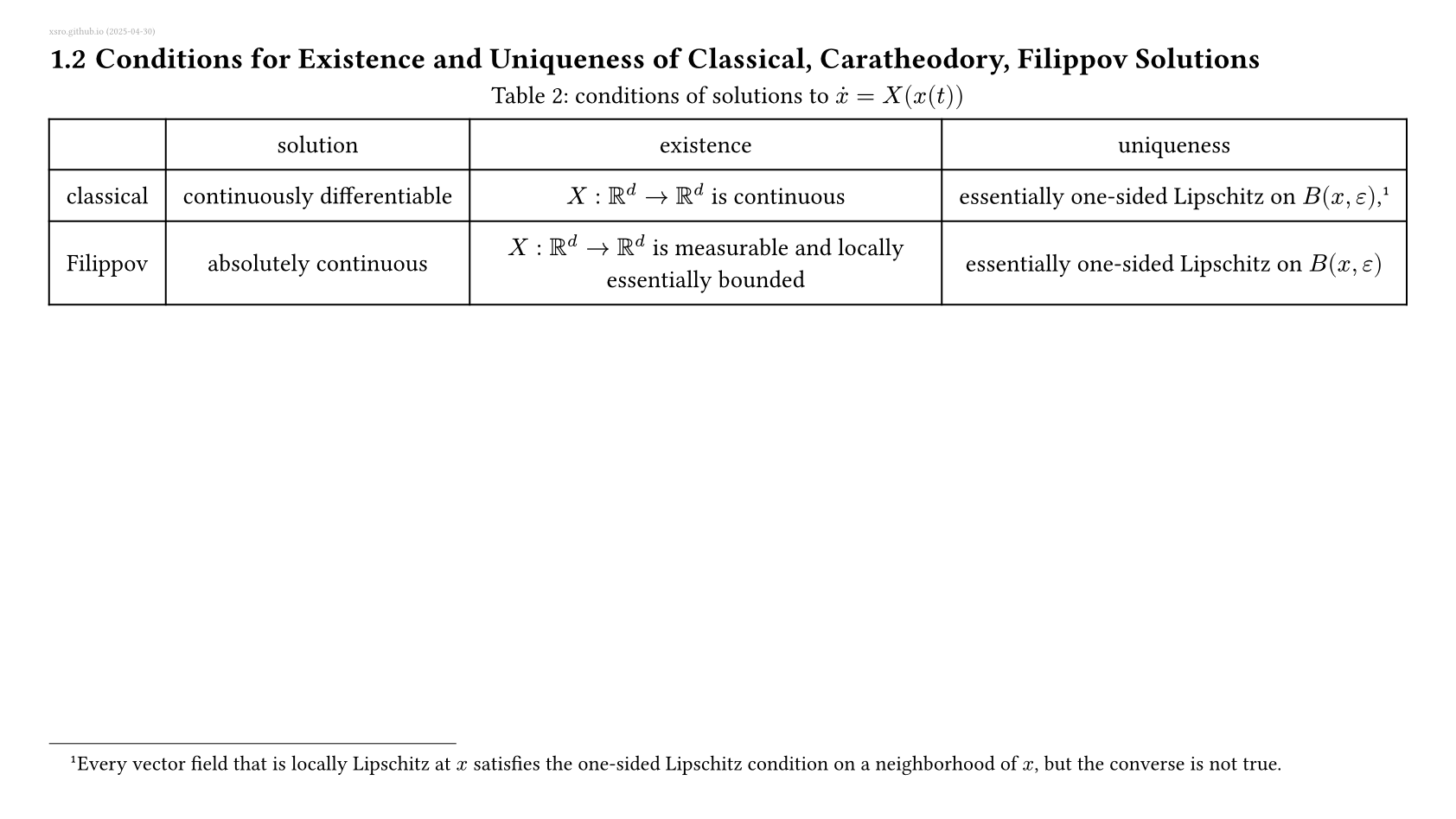
Proposition 3 令$X:\mathbb{R}^d\to\mathbb{R}^d$是一个可测的、局部本性有界的映射。 然后,对于所有$x_0\in \mathbb{R}^d$,存在一个从$x(0)=x_0$开始的(10)的Filippov解。
这里局部本性有界(locally essentially bounded)指在每个点的有界邻域上都有界,这里的邻域要排除测度为零的集合。 该条件等价于微分包含的caratheodory解条件。 也就是说满足该条件的微分方程可以通过(19)转换为Filippov微分包含。